An Introduction to Continuations
I'm going to introduce to you the concept of continuations. It's been said, "continuations are one of the most bizarre inventions in the history of computer science." I would say that they are bizarre, and difficult to explain, but when you understand what they are, you'll realize that you've been using the concept since you first learned how to compute complex binary operations in primary school.
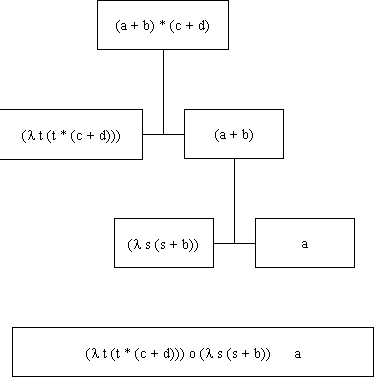
(a + b) * (c + d)
A tree structure is used to illustrate the steps a computer would take with regards to the variable a.

In level two, the intermediate value t is introduced and substituted for the expression (a + b). The computer isolates (a + b) and attempts to evaluate it.
In level three, yet another intermediate value is introduced, substituted in place of a. Once it's determined a value for this variable, as well as b, c, and d on other branches of evaluation, the computer then can begin substituting these values back into the succession of continuations until it arrives at a final value.
As you can see, this entire tree can be represented as the composition of both lambda functions when the value for a is substituted back in for s. The lambda functions are considered the continuations, that is, they are what to do with computed value a in the future of the computation.
Continuations can be described as like exceptions, like those used in Java. An exception signals that a special case was encountered in the course of execution of a program. Once an exception has been raised, the statically nested blocks break or terminate one by one until the program ends or the exception is caught. This occurs in much the same way that a value bound to a continuation can be thrown to another continuation that knows what to do with it, that is, continue the computation of an expression. Consider the following abstract example, written in Java syntax:
try{
//This is a block of statements, within the main method, any or all of which could throw an exception.
if ( /* some condition that could cause a problem in the program */)
throw new exceptionName();
}
catch (ExceptionName ParameterName){
//Block of statements to be executed if the exceptionName exception is thrown in try
//Notice that this catch resides outside of the the try block, but still within the main method.
}
//...maybe other catch blocks
is similar to
funcOrProc(currCont){
//This block of statements will execute, until some code calls or passes a value to the continuation,
//similar to how an exception is throw.
if ((* some condition occurs *))
(* pass a value into currCont(value) and exit this block *)
}
currCont(value){
(* do something with the value that's been passed *)
(* notice that this block is outside of the block where the value it's being passed came from *)
(* it represents the future of that value in the computation. *)
Continuations have also been likened to a goto, in that once you obtain a missing value required by a computation, you actually break out to another portion of code that's already been parsed and stored away as a continuation to continue its evaluation.
10 INPUT A 20 GOTO 50 30 *** REM *** THIS GOTO, BEING THAT ALL VARIABLES IN BASIC ARE GLOBAL, HAS THE EFFECT OF PASSING THE VALUE A 35 *** REM *** TO LINE 50, WHICH REPRESENTS THE CONTINUATION IN THAT IT IS THE FUTURE OF THE VALUE A IN THE 40 *** REM *** ENTIRE COMPUTATION. 50 LET B = 5 60 LET C = A + B 70 PRINT C
In Scheme, call/cc or its long-hand equivalent call-with-current-continuation mean just that, to call with current continuation.
(call/cc (lambda (k) (* 5 4))) -> 20
In this first example, the continuation is obtained by call/cc, but since it is never used in the expression, the result returned is simple the product of 4 and 5, 20.
(call/cc (lambda (k) (* 5 (k 4)))) -> 4
In this example, the continuation passed in is used and k is bound to it, but since it is before the multiplication, the value returned is the value bound to the continuation, 4.
(+ 2 (call/cc (lambda (k) (* 5 (k 4))))) -> 6
In this example, the continuation k passed in include the addition of 2, so, since the continuation is bound to and therefore returns the value 4, as in the previous example, its continuation include the addition of 2, so, 2 plus 4 is 6.
(define product
(lambda (ls)
(call/cc
(lambda (break)
(let f ((ls ls))
(cond
(( null? ls) 1)
(( = (car ls) 0) (break 0))
(else ( * (car ls) (f (cdr ls))))))))))
(product '(1 2 3 4 5)) -> 120
(product '(7 3 8 0 1 9 5)) -> 0
In this example, the continuation break is passed into the call/cc function so that, if the function encounters a 0 at any point during its execution, it can break out of the recursive loop and return a 0. Otherwise, it will continue to recursively multiply the head of the list (car) with the product of the elements of the tail of the list (cdr).
As you can see, the use of an explicit continuation in this case will save the function time in that if it encounters a zero, it won't have to continue to process the rest of the data because the product will always be zero in that case.
A very good page about call/cc in Scheme
This paper is divided into six sections:
Scheme Introduction
Scheme Lexer (Scanner) with explanation
Scheme Yacc Parser with explanation
Scheme Semantic Structure with explanation
Special Feature: Continuations and their use in Scheme
An Example of a Scheme program